使用basic_rnn_seq2seq拟合曲线 - Tensorflow

TensorFlow虽然对Seq2Seq的框架的封装只用一个函数就完成了。但是，Seq2Seq的这个函数用起来并不友好，跟我们以前使用的TensorFlow中的函数并不是一样，所以有必要通过例子来演示一下。本例中使用2层的GRU循环网络，每层有12个节点。编码器与解码器中使用同样的网络结构。

实例描述

通过sin与con进行叠加变形生成无规律的模拟曲线，使用Seq2Seq模式对其进行学习，拟合特征，从而达到可以预测下一时刻数据的效果。该例子共分为以下几步。

1．定义模拟样本函数

本例中通过函数制作规则的曲线来验证网络模型；定义两个曲线sin和con，通过随机值将其变形偏移，将两个曲线叠加。具体代码如下。

代码9-30 基本Seq2Seq

import random
import math

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt


def do_generate_x_y(isTrain, batch_size, seqlen):
    batch_x = []
    batch_y = []
    for _ in range(batch_size):
        offset_rand = random.random() * 2 * math.pi
        freq_rand = (random.random() - 0.5) / 1.5 * 15 + 0.5
        amp_rand = random.random() + 0.1

        sin_data = amp_rand * np.sin(np.linspace(
            seqlen / 15.0 * freq_rand * 0.0 * math.pi + offset_rand,
            seqlen / 15.0 * freq_rand * 3.0 * math.pi + offset_rand, seqlen * 2))

        offset_rand = random.random() * 2 * math.pi
        freq_rand = (random.random() - 0.5) / 1.5 * 15 + 0.5
        amp_rand = random.random() * 1.2

        sig_data = amp_rand * np.cos(np.linspace(
            seqlen / 15.0 * freq_rand * 0.0 * math.pi + offset_rand,
            seqlen / 15.0 * freq_rand * 3.0 * math.pi + offset_rand, seqlen * 2)) + sin_data

        batch_x.append(np.array([sig_data[:seqlen]]).T)
        batch_y.append(np.array([sig_data[seqlen:]]).T)

    # 当前shape: (batch_size, seq_length, output_dim)
    batch_x = np.array(batch_x).transpose((1, 0, 2))
    batch_y = np.array(batch_y).transpose((1, 0, 2))
    # 转换后shape: (seq_length, batch_size, output_dim)

    return batch_x, batch_y


# 生成15个连续序列，将con和sin随机偏移变化后的值叠加起来
def generate_data(isTrain, batch_size):
    seq_length = 15
    if isTrain:
        return do_generate_x_y(isTrain, batch_size, seq_length)
    else:
        return do_generate_x_y(isTrain, batch_size, seq_length * 2)

将该曲线按照30个序列一组的样式组成训练用的样本。30个序列分成了两部分：

• 一部分当成现在的序列batch_x
• 一部分当成将来的序列batch_y。

2．定义参数及网络结构

前面介绍过basic_rnn_seq2seq的输入是一个list，这与我们平时遇到过的模型不太一样，所以需要构建一个list，以方便传入basic_rnn_seq2seq中。

在代码中，定义3个list(encoder_input、expected_output、decode_input)，按照时间序列的数量来循环创建占位符，并使用append方法放入到list中。

网络模型定义为2层的循环网络，每层12个GRUcell。用MultiRNNCell将cell定义好后与前面的list一起传入basic_rnn_seq2seq中。

生成的结果为dec_outputs，dec_outputs中为每个时刻有12个GRUcell的输出，所以还需要通过循环在每个时刻下加一个全连接层，将其转为输出维度output_dim（output_dim=1）的节点。

代码9-30 基本Seq2Seq（续）

sample_now, sample_f = generate_data(isTrain=True, batch_size=3)
print("training examples : ")
print(sample_now.shape)
print("(seq_length, batch_size, output_dim)")

seq_length = sample_now.shape[0]
batch_size = 10

output_dim = input_dim = sample_now.shape[-1]
hidden_dim = 12
layers_num = 2

# 学习率
learning_rate = 0.04
nb_iters = 100

lambda_l2_reg = 0.003  # L2 regularization of weights - avoids overfitting

tf.reset_default_graph()

encoder_input = []
expected_output = []
decode_input = []
for i in range(seq_length):
    encoder_input.append(tf.placeholder(tf.float32, shape=(None, input_dim)))
    expected_output.append(tf.placeholder(tf.float32, shape=(None, output_dim)))
    decode_input.append(tf.placeholder(tf.float32, shape=(None, input_dim)))

tcells = []
for i in range(layers_num):
    tcells.append(tf.contrib.rnn.GRUCell(hidden_dim))
Mcell = tf.contrib.rnn.MultiRNNCell(tcells)

dec_outputs, dec_memory = tf.contrib.legacy_seq2seq.basic_rnn_seq2seq(encoder_input, decode_input, Mcell)

reshaped_outputs = []
for ii in dec_outputs:
    reshaped_outputs.append(tf.contrib.layers.fully_connected(ii, output_dim, activation_fn=None))

3．定义loss函数及优化器

为了防止过拟合，对basic_rnn_seq2seq循环网络中的参数使用了l2_loss正则，由于最后一个全连接只是起到转化作用，就忽略不做l2_loss正则了（也可以加上，效果没有影响）。L2的调节因子设为0.003，学习率设为0.04。

代码9-30 基本Seq2Seq（续）

#计算L2的loss值
output_loss = 0
for _y, _Y in zip(reshaped_outputs, expected_output):
    output_loss += tf.reduce_mean(tf.pow(_y - _Y, 2))

# 求正则化loss值
reg_loss = 0
for tf_var in tf.trainable_variables():
    if not ("fully_connected" in tf_var.name):
        # print(tf_var.name)
        reg_loss += tf.reduce_mean(tf.nn.l2_loss(tf_var))

loss = output_loss + lambda_l2_reg * reg_loss
train_op = tf.train.AdamOptimizer(learning_rate).minimize(loss)

预测结果与真实结果的平方差再加上l2的loss值，作为输出的loss值。优化器同样使用AdamOptimizer。

4．启用session开始训练

在session中将训练和测试单独封装成了两个函数。在train_batch函数里先取指定批次的数据，通过循环来填充到encoder_input和expected_output列表里。

代码9-30 基本Seq2Seq（续）

sess = tf.InteractiveSession()

def train_batch(batch_size):
    X, Y = generate_data(isTrain=True, batch_size=batch_size)
    feed_dict = {encoder_input[t]: X[t] for t in range(len(encoder_input))}
    feed_dict.update({expected_output[t]: Y[t] for t in range(len(expected_output))})
    c = np.concatenate(([np.zeros_like(Y[0])], Y[:-1]), axis=0)  # 来预测最后一个序列
    feed_dict.update({decode_input[t]: c[t] for t in range(len(c))})
    _, loss_t = sess.run([train_op, loss], feed_dict)
    return loss_t

def test_batch(batch_size):
    X, Y = generate_data(isTrain=True, batch_size=batch_size)
    feed_dict = {encoder_input[t]: X[t] for t in range(len(encoder_input))}
    feed_dict.update({expected_output[t]: Y[t] for t in range(len(expected_output))})
    c = np.concatenate(([np.zeros_like(Y[0])], Y[:-1]), axis=0)  # 来预测最后一个序列
    feed_dict.update({decode_input[t]: c[t] for t in range(len(c))})
    output_lossv, reg_lossv, loss_t = sess.run([output_loss, reg_loss, loss], feed_dict)
    print("-----------------")
    print(output_lossv, reg_lossv)
    return loss_t

# 训练
train_losses = []
test_losses = []

sess.run(tf.global_variables_initializer())
for t in range(nb_iters + 1):
    train_loss = train_batch(batch_size)
    train_losses.append(train_loss)
    if t % 50 == 0:
        test_loss = test_batch(batch_size)
        test_losses.append(test_loss)
        print("Step {}/{}, train loss: {}, \tTEST loss: {}".format(t, nb_iters, train_loss, test_loss))
print("Fin. train loss: {}, \tTEST loss: {}".format(train_loss, test_loss))

# 输出loss图例
plt.figure(figsize=(12, 6))
plt.plot(np.array(range(0, len(test_losses))) /
         float(len(test_losses) - 1) * (len(train_losses) - 1),
         np.log(test_losses), label="Test loss")

plt.plot(np.log(train_losses), label="Train loss")
plt.title("Training errors over time (on a logarithmic scale)")
plt.xlabel('Iteration')
plt.ylabel('log(Loss)')
plt.legend(loc='best')
plt.show()

对于decode_input的输入要重点说明一下，将其第一个序列的输入变为0，作为起始输入的标记，接上后续的Y数据（未来序列）作为解码器部分的Decoder来输入。由于第一个序列被占用了，保证总长度不变的情况下，Y的最后一个序列没有作为Decoder的输入。但是输出时会有关于未来序列预测的全部序列值，并在计算loss时与真实值Y进行平方差。

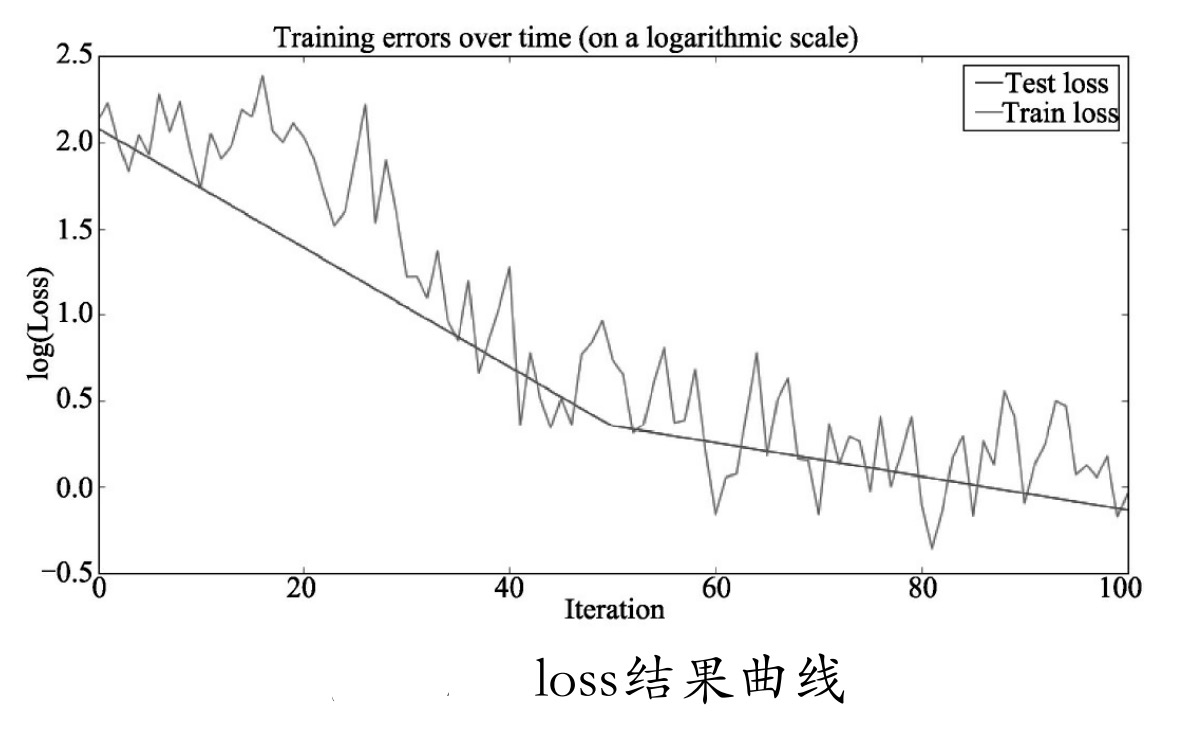
最终将loss值通过plot打印出来，生成结果如下，loss结果曲线如图9-28所示。

training examples :
(15, 3, 1)
(seq_length, batch_size, output_dim)
-----------------
7.66522 113.373
Step 0/100,train loss: 8.341724395751953, TEST loss:8.005338668823242
-----------------
1.11881 99.788
Step 50/100,train loss:2.0858113765716553, TEST loss:1.418175220489502
-----------------
0.618375 83.6507
Step 100/100,train loss:0.9577032327651978, TEST loss:0.8693273067474365
Fin. train loss:0.9577032327651978, TEST loss:0.8693273067474365

5．准备可视化数据

一般情况下，将整个输出值进行显示即可。但这里考虑到要配合使用时的演示，因此我们需要模型来预测未来序列，即没有decode_input的输入。前面说了，这种情况可以将decode_input全设为0，但其识别效果不客观。为了模型可用，可以将预测值范围稍加改变，只预测之后一次时间序列的值。例如，知道前面的所有序列，预测当天股票的收盘价格、开盘价格等。这也是非常实际的应用。

于是在可视化部分，取时间序列2倍的样本，前一倍用于输入模型，会产生最后一天的预测值，同时也将后一倍的数据显示出来，用于比对每个序列的预测值。

代码9-30 基本Seq2Seq（续）

# 测试
nb_predictions = 5
print("visualize {} predictions data:".format(nb_predictions))

preout = []
X, Y = generate_data(isTrain=False, batch_size=nb_predictions)
print(np.shape(X), np.shape(Y))
for tt in range(seq_length):
    feed_dict = {encoder_input[t]: X[t + tt] for t in range(seq_length)}
    feed_dict.update({expected_output[t]: Y[t + tt] for t in range(len(expected_output))})
    c = np.concatenate(([np.zeros_like(Y[0])], Y[tt:seq_length + tt - 1]), axis=0)  # 从前15个的最后一个开始预测

    feed_dict.update({decode_input[t]: c[t] for t in range(len(c))})
    outputs = np.array(sess.run([reshaped_outputs], feed_dict)[0])
    preout.append(outputs[-1])

print(np.shape(preout))  # 将每个未知预测值收集起来准备显示出来。
preout = np.reshape(preout, [seq_length, nb_predictions, output_dim])

前15次时间序列用于输入，后15次循环来使用模型预测，每次都将输出的最后一个时间序列收集起来，最终得到15个时间序列批次的预测结果preout。

6．画图显示数据

将批次设为4，随机取4个序列片段，每个片段的15个序列预测以图像形式显示出来。

代码9-30 基本Seq2Seq（续）

for j in range(nb_predictions):
    plt.figure(figsize=(12, 3))

    for k in range(output_dim):
        past = X[:, j, k]
        expected = Y[seq_length - 1:, j, k]  # 对应预测值的打印

        pred = preout[:, j, k]

        label1 = "past" if k == 0 else "_nolegend_"
        label2 = "future" if k == 0 else "_nolegend_"
        label3 = "Pred" if k == 0 else "_nolegend_"
        plt.plot(range(len(past)), past, "o--b", label=label1)
        plt.plot(range(len(past), len(expected) + len(past)),
                 expected, "x--b", label=label2)
        plt.plot(range(len(past), len(pred) + len(past)),
                 pred, "o--y", label=label3)

    plt.legend(loc='best')
    plt.title("Predictions vs. future")
    plt.show()

为了跟真实的序列值比较，这里将真实的序列值也从15个序列开始打印出来，index=14的值即为预测的第一个值。运行上面的代码，结果如所示。

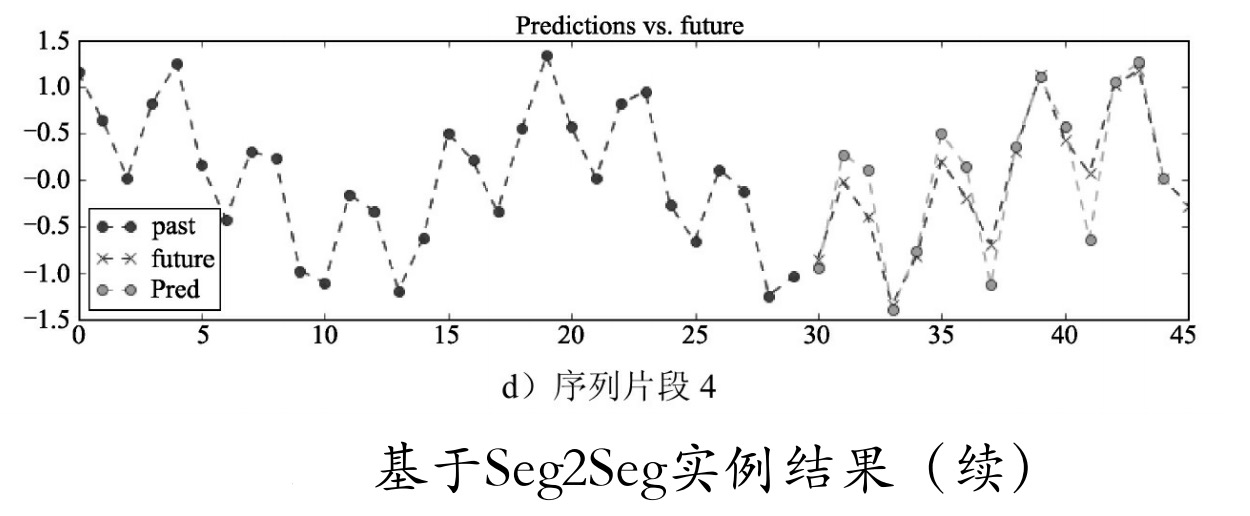
可以看到，生成的预测数据与真实数据相差并不大。

注意： 这里使用了feed_dict的update方法来处理复杂的feed_dict的情况，通过Update可以在原有的feed_dict中加入新的feed数据，将一行语句变为多行输入